Bootstrap Your Own Latent: Self-Supervised Learning Without Contrastive Learning

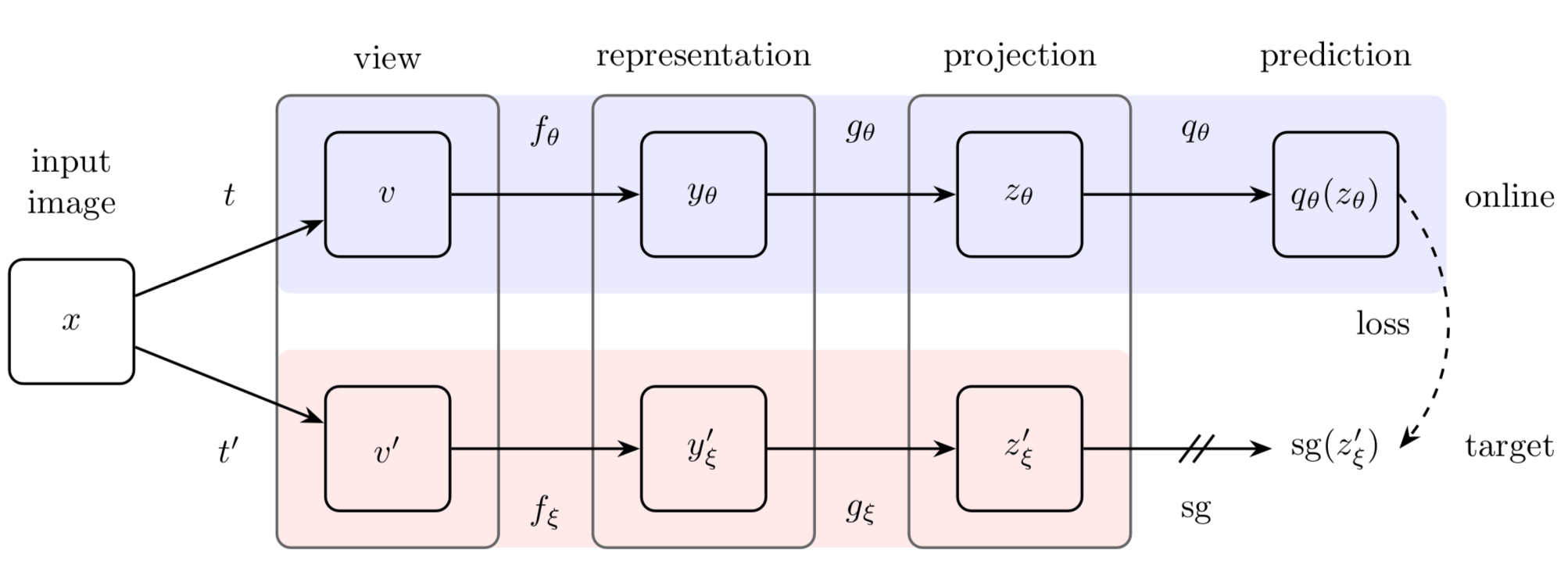
Introduction

Supervised Learning is the top solution to train Convolutional Neural Network (CNN), which is the model made to solve computer vision like self-driving car, security, automatization, etc. As these computer vision tasks increase, the need to improve these systems also emerges.

One of the main ways to improve these systems is through having more data and bigger models, but unfortunately by using supervised learning these solutions need labeled data (information that has been classified by humans), which makes them expensive and difficult to get.

The bottleneck that limits the process of training is the process itself. Since supervised learning is dependent on label data which limits the amount of information the model are trained on. This represents a big limitation on the training of these models and a waste of unlabeled data. Current research on Self-Supervised Learning is able to train model without label data and take out the need of using Contrastive Learning which is the most common way to train model with Self-Supervised Learning.

Self-Supervised Learning

Self-Supervised learning gained popularity on the training of Large Language models, by having the model learn from many unlabeled data which make the model learn the general structure of the words and their meaning. With that general knowledge then these pre-trained models are use for transfer learning to solve more specific take.

Transfer Learning

Transfer learning is the process of using a model like CNNs trained on a large corpus of labeled data to gain a general structure and meaning of images and then use it to solve a more specific tasks. The use of large label data is to ensure the model learns a broad variety of images. Normally transfer learning is used when there is a limited amount of data, limited computational power or the improvement of performance. Even do it seems that transfer learning can solve the problem of using datasets with small label data still it does not. Since a key component of using transfer learning is its implementation, the data needs to be similar or close to the large corpus of data that was used to train the model.

Since more research has been done on training CNNs with self-supervised learning, there has been new approaches to make able CNN learn from unlabeled data. One of these approaches was introduced by the paper called bootstrap your own latent where demonstrates that is not necessary of use contrastive learning approach for a self-supervised setting.

Contrastive Learning

The idea of contrastive learning is to make a model learn an embedding space that captures the essential information about its inputs including their structure and semantics.

Example: The model $f_\theta$ w have an image input of 224 pixels by 224 pixels which have $[24*24] = 576$ dimensions. The model outputs a vector that represents the input of $16$ dimensions which occupies 36 times less space than the image with almost the same information.

This is done by training the model to output vector representations that are close for similar examples and farther apart when there are different examples. To train the model three type exampled we use: the anchor example (image as a reference), a positive example (image closely related to the anchor example) and a negative example (an image that is not related to the anchor example).

Example: Imagine the task to create a model that discriminate between animals and non-animals. The inputs for the model will be an image of a dog, cat and a watermelon. The anchor example $x^a$(dog), positive example $x^+$ (cat) and the negative example $x^-$ (watermelon). The model which has a CNN denoted as $f_\theta$ (CNN is the one that gets the structure and meaning of the image) and a projection $g_\theta$ (a projection head is applied to map the representations of $f_\theta$ to its loss function). When the image of a dog and a cat is imputed to the model it should output similar vector representations

And vice-versa when the negative example is inputted to the model the vector representation is completely different and far from the representation of the anchor image.

The paper A Simple Framework for Contrastive Learning of Visual Representations(SimCLR) is the foundation on implementing contrastive methods for self-supervised learning. In the paper SimCLR was introduced a loss called NT-Xent which was originally inspired on the InfoNCE just having $\tau$ temperature variable as a modification.

InfoNCE $\ell_{i,j} = - \log \frac{\exp(\text{sim}(z_i, z_j)/\tau)}{\sum_{k=1}^{2N} \mathbf{1}_{[k \neq i]} \exp(\text{sim}(z_i, z_k)/\tau)}$

The InfoNCE loss will enforce $x^a$ and $x^+$ to be similar pairs and also enforce pairs that are different. The sim(.) function is a similarity metric which measures how a vector is similar against others. This metric is used to minimize the difference between positive pairs $(x^a, x^x)$ and maximize the distance between negative pairs $(x^a, x^-)$

In summary, we can think of contrastive tasks as trying to generate similar representation for positive examples and different for negative examples.

Bootstrap Your Own Latent: BYOL

In contrastive learning positive examples are easy to obtain, but negative examples are difficult to get. Positive examples can be just a modified version of the anchor image. Negative examples can be difficult to get because we to define what this is different to an anchor and have enough similarity to make a challenging to the model without human intervention.

For this reason there is research of self-supervised learning without contrastive learning. This is difficult because there is a need for negative example, if not what can stop the model of generating the same vector representation in contrast to an anchor example and positive example which is called collapse. For negative examples the model is forced to learn meaning representations for its inputs.

In order to understand how BYOL archive self-supervised learning without contrastive methods let’s explore the main components of this self-supervised learning framework.

BYOL have two neural networks, named as online and target networks that are able to interact to each other. The model is trained by the online network to predict the target network representation with the same image using different augmented views.

To generate this augmented views, we create 2 distortionated copies form an input image, by applying two sets of data augmentation operations. The transformation includes

• random cropping: a random patch of the image is selected, with an area uniformly sampled between 8% and 100% of that of the original image, and an aspect ratio logarithmically sampled between 3/4 and 4/3. This patch is then resized to the target size of 224 × 224 using bicubic interpolation;
• Random horizontal flip: optional left-right flip;
• color jittering: the brightness, contrast, saturation and hue of the image are shifted by a uniformly random offset applied on all the pixels of the same image. The order in which these shifts are performed is randomly selected for each patch;
• color dropping: an optional conversion to grayscale. When applied, output intensity for a pixel (r,g,b) corresponds to its luma component, computed as $0.2989r+ 0.5870g+ 0.1140b$;
• Gaussian blurring: for a 224 × 224 image, a square Gaussian kernel of size 23 ×23 is used, with a standard deviation uniformly sampled over $[0.1,2.0]$;
• solarization: an optional color transformation $x→x·1{x<0.5}+ (1−x)·1{x≥0.5}$ for pixels with values in $[0,1]$.

Credits: Bootstrap your own latent: A new approach to self-supervised Learning

These augmentations double the examples, if we have a batch of 32 images, we end up with 64 images per batch.

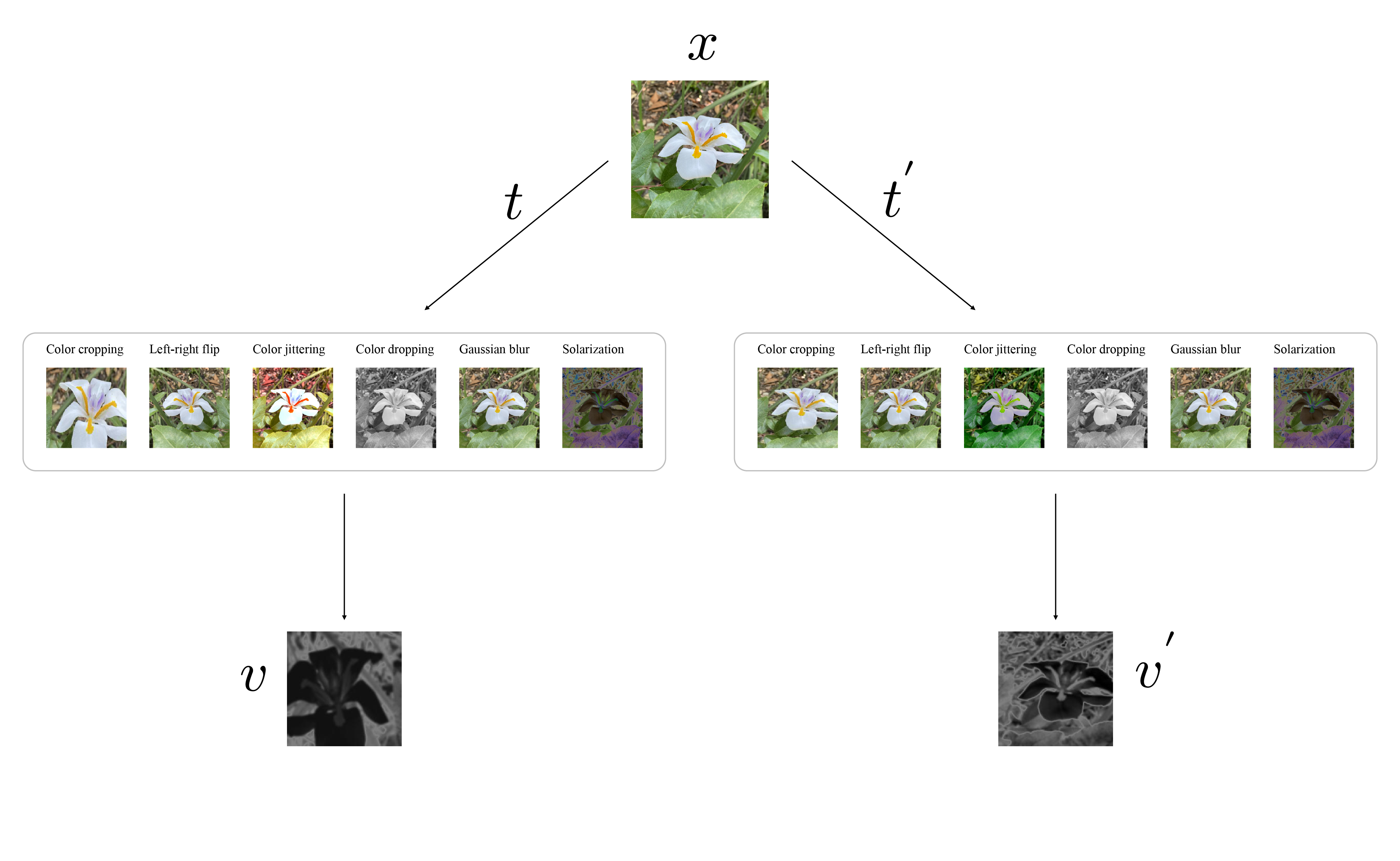
Data augmentation is used to force the model to learn invariant representations which means that independently of the transformation imposed to an input the model will generate the same representations.

The online network have parameters $\theta$ updated by back propagation and is made from three components: an encoder $f_{\theta}$, projector $g_{\theta}$ and predictor $q_{\theta}$. The target network have an encoder $f_{\xi}$ and projector $g_{\xi}$. The parameters $\xi$ of the target network are not updated by back propagation, but instead the model is updated by Exponential Moving Average (EMA) of the online parameters $\theta$. The parameters of the target network can be seen a smoothed version of the online network.

${\xi}\longleftarrow{\tau}{\xi}+(1-\tau){\theta}$

$\tau$ is the decay rate $T\in[0, 1]$

The representation head uses a ResNet-50 for $f_{\theta}$ and $f_{\xi}$. The ResNet-50 receives the augmented image of size (224, 224, 3) and output a vector representation or a vector embedding of 2048-dimensional for the online network $y_{\theta}$ and for the target network $y_{\xi}^{‘}$. Then a projection head $g$ receives the vector $y$ and produces the final output for the target network $sq(z_{\xi}^{‘})$. $sg$ means stop gradient, which the parameters $\xi$ for the target network will not be updated by back-propagation. The output $z_{\theta}$ of the projection head $g_{\theta}$ of the online network is inputted to the prediction head $q_{\theta}$ which produces the final output $q_{\theta}(z_{\theta})$ of the online network. The projection and prediction heads consist of a linear layer with an input shape of 2048-dimensions and output size of 4096 followed by batch normalization, a non-linear function (ReLU) and a final layer with output of dimension 256.

The projection and predictions heads are multi-layer perceptron (MLP)

Credits: Bootstrap your own latent: A new approach to self-supervised Learning

Training

BYOL is train to minimizes the similarity loss between $q_{\theta}(z_{\theta})$ and $sq(z_{\xi}^{‘})$. The loss function is defined as: \(\mathcal{L}_{\theta, \xi} \triangleq \left\| \overline{q_{\theta}(z_0)} - \overline{z'_{\xi}} \right\|_2^2 = 2 - 2 \cdot \frac{\langle q_{\theta}(z_0), z'_{\xi} \rangle}{\| q_{\theta}(z_0) \|_2 \cdot \| z'_{\xi} \|_2}\)

$q_{\theta}(z_{\theta})$ and $z_{\xi}^{‘}$ are normalized to be unit vectors, \(\overline{q}_{\theta}(z_{\theta}) = \frac{q_{\theta}(z_{\theta})}{\| q_{\theta}(z_0)\|_2}\) and \(\overline{z}_{\xi}^{'} = \frac{z^{'}_{\xi}}{\| z_{\xi}^{'} \|_2}\) . Then is applied a mean squared error between the normalized outputs of the online and target networks.

The loss \(\mathcal{L}_{\theta,\xi}\) is computed from feeding $v$ to the online network and $v’$ to the target network. The loss is symmetrized by calculating \(\tilde{\mathcal{L}}_{\theta,\xi}\) by feeding $v’$ to the online network and $v$ to the target network.
\(\mathcal{L}^{BYOL}_{\theta, \xi} = \mathcal{L}_{\theta,\xi} + \tilde{\mathcal{L}}_{\theta,\xi}\)

The symmetrization of the loss makes each network, online and target have the same data to learn from. Since both networks share the same data it ensures that will have an equal contribution to the total loss. This promotes more robust and generalized features, since the model captures a wider range of data variations.

For each training step is performed a $optimatizer$ algorithm to minimize $\mathcal{L}^{BYOL}_{\theta, \xi}$ with respect only to $\theta$. \({\theta}\longleftarrow\text{optimizer}(\theta, \nabla_{\theta}{\tilde{\mathcal{L}}_{\theta,\xi}}, {\eta})\) \({\xi}\longleftarrow{\tau}{\xi}+(1-\tau){\theta}\)

$\eta$ is the learning rate

In the framework BYOL the LARS optimizer is used update $\theta$, with a cosine decay learning rate schedule, more information on the BYOL paper. After the training, the encoder of the online network $f_{\theta}$ is used to produce representations.

Why BYOL do not collapse

These are the two main reasons why BYOL do not collapse.

In the paper On the Importance of Asymmetry for Siamese Representation Learning explained the importance of the asymmetry designs (BYOL) in self-supervised frameworks. The representations outputted by the model improves when the source encoder in this case the online encoder it updated via gradient decent and the target encoder is updated by the source encoder weights. The outputs of target act as a judge of the quality of the output source. Also in the paper was proven in some level that keeping a relatively lower variance in target encodings than source can help representation learning. BYOL archive this low variance by updating the weight of the target network using EMA.

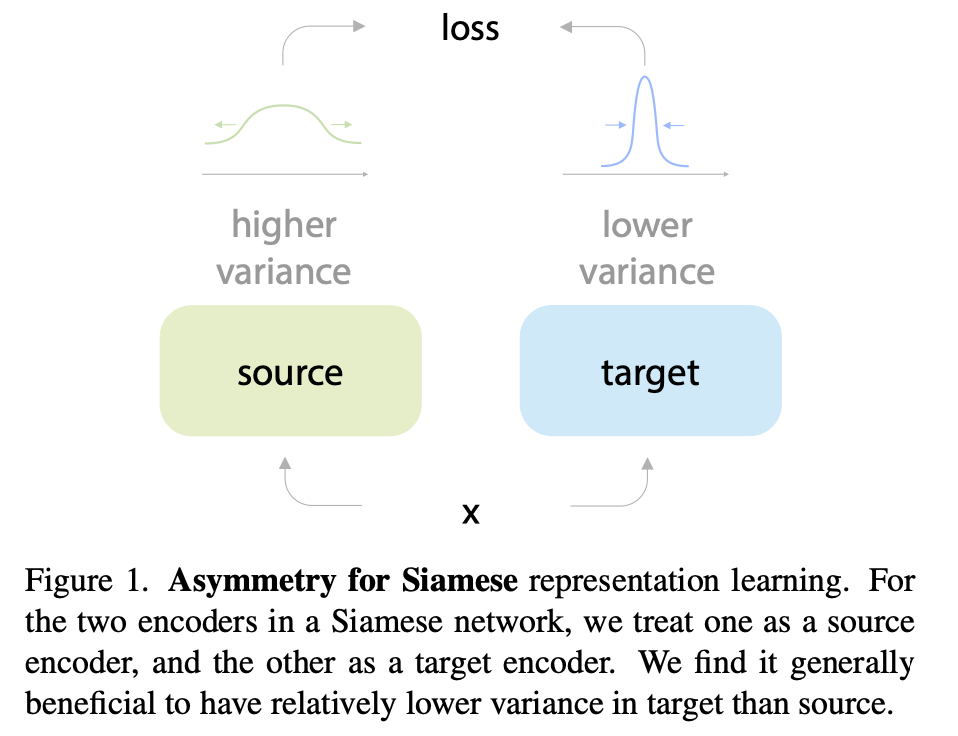Credits: On the Importance of Asymmetry for Siamese Representation Learning

In the post Understanding self-supervised and contrastive learning with “Bootstrap Your Own Latent” (BYOL) is explained the importance of Batch Normalization in the prevention of collapse. They notice that if batch norm was not in the MLP the model will perform poorly. Batch norm standardize the activations in the network based on the batch’s mean and variance, which can vary between batches. Since the online and target network have different parameters in the batch norm layer, the output representation of the online and target network will also differ. These slightly differences in the outputs force the model to generate rich representations. However, is also highlighted that is worth avoiding batch normalization and use other alternatives like layer normalization or weight standardization with group normalization.

Results

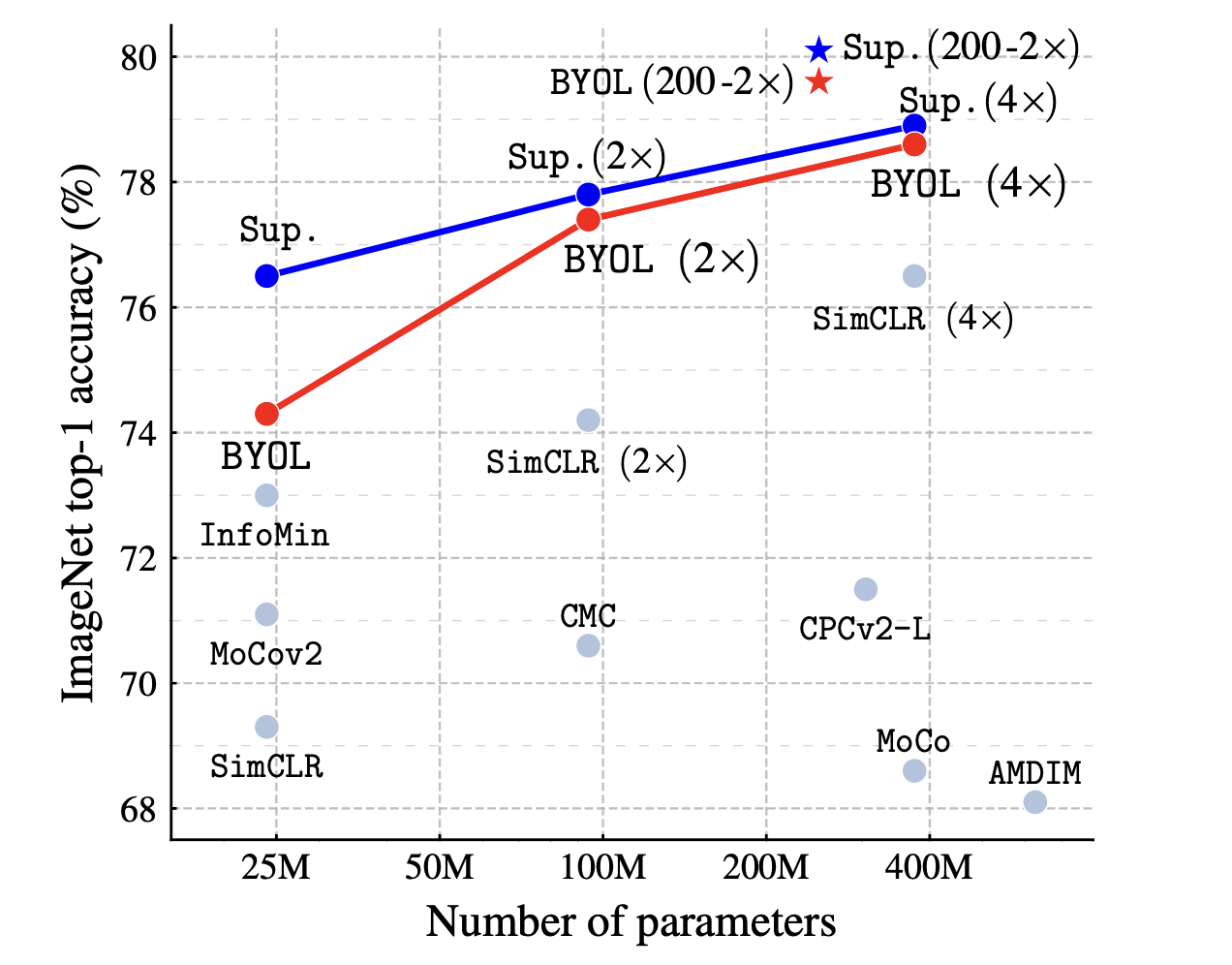
The BYOL framework archive higher performance than the state-of-the-art contrastive methods in the ImageNet dataset. Credits: Bootstrap your own latent: A new approach to self-supervised Learning

BYOL is evaluated in both linear evaluation and fine-tuning evaluation. The linear evaluation consists on training a multinomial logistic regression on top of the frozen representations outputted by the encoder $f_\theta$ (The encoder weights are not trained in this evaluation.).

To fine-tune evaluation consist on initialize $f_\theta$ parameters with the pre-trained representation, and retrain the encoder alongside a classifier on labeled dataset.

Note: For fine-tune there are many other types of architecture that can be used to fine tune this model.

BYOL was pre-trained on ImageNet by 300 epochs. After pre-trained, the model is evaluated on many downstream tasks by using linear and fine-tune evaluations. 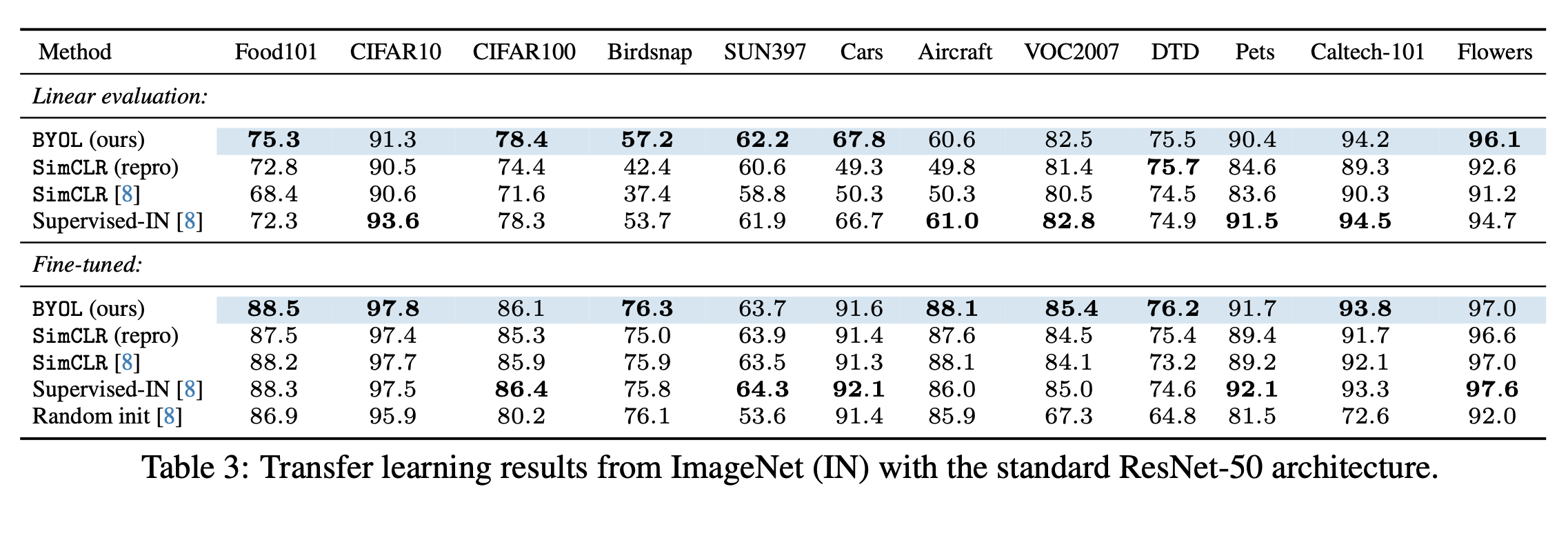Credits: Bootstrap your own latent: A new approach to self-supervised Learning This result show competitive results to the Supervised training of RestNet-50 in ImageNet and surpass the performance of contrastive learning models.

In these tables shows the robustness of BYOL against batch size compared to SimCLR. Also show the robustness for data augmentations showing that is not that sensitive to the choice of image augmentation like SimCLR. 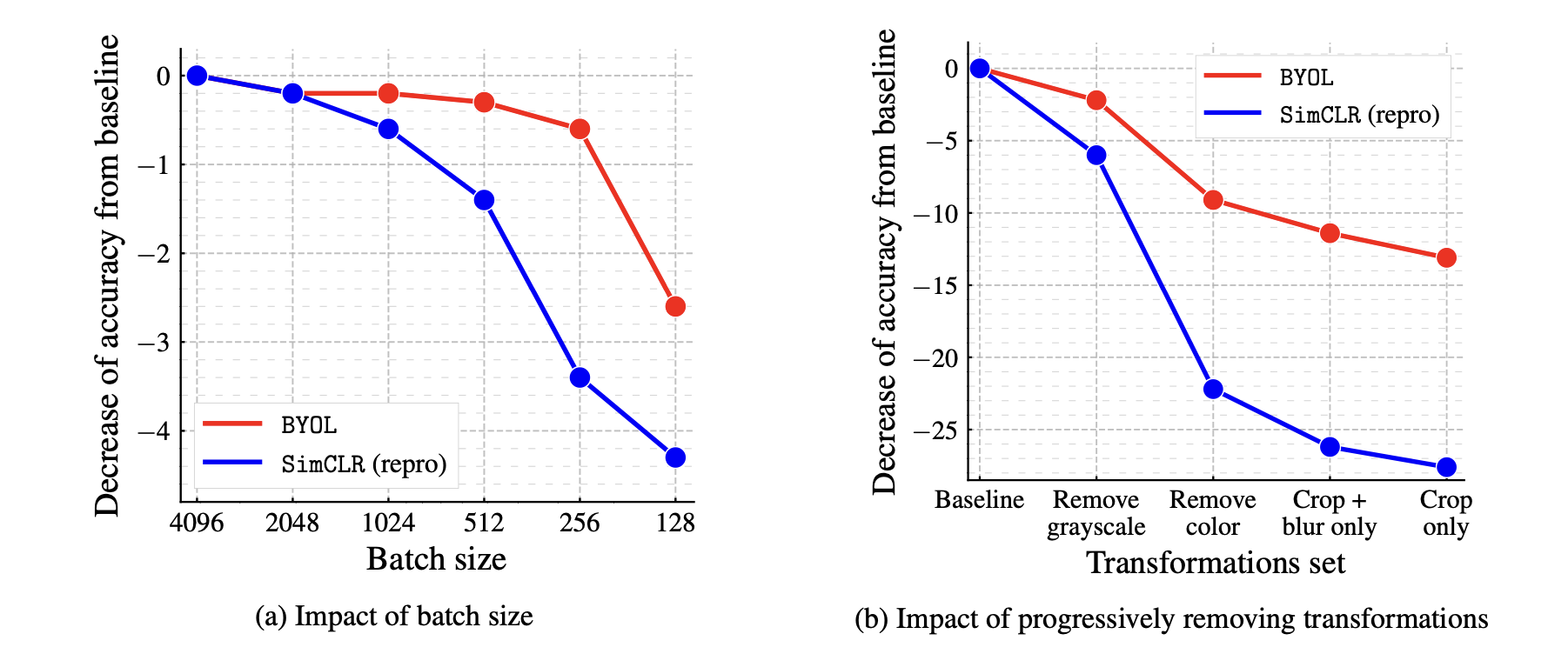Credits: Bootstrap your own latent: A new approach to self-supervised Learning

Remarks

BYOL gives another solution to the traditional use of contrastive loss for self-supervised frameworks. Giving more research on this non-contrastive framework opens the door for more powerful models. Also taking out the need of negative examples gives more freedom to the model to understand the data and give richer representations.

In the original BYOL paper have many other interesting topics:

• Result on linear and semi-supervised evaluation on ImageNet.
• A more detail information about the setup of BYOL.
• Details on the relation to contrastive methods.
• Pseudo-code in JAX to implement BYOL.

I encourage you to look the papers from the reference section. This will give you a broader perspective on the Bootstrap your own latent: A new approach to self-supervised Learning paper.

Thank you for reading!

Cite as:

@article{
  tajia2024bootstrap,
  title={Bootstrap Your Own Latent},
  author={Tajia, Pedro},
  year={2024},
  howpublished={\url{https://pedrotajia.com/2024/10/20/bootstrap-your-own-latent.html}}
}

References

1. Jean-Bastien Grill et al., “Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning”, arXiv, 2020.
2. Ting Chen et al., “A Simple Framework for Contrastive Learning of Visual Representations (SimCLR)”, arXiv, 2020.
3. Xinlei Chen and Kaiming He, “On the Importance of Asymmetry for Siamese Representation Learning”, arXiv, 2022.
4. Imbue Research, “Understanding Self-Supervised and Contrastive Learning with ‘Bootstrap Your Own Latent’ (BYOL)”, Blog post.
5. Thalles Silva, “Exploring SimCLR: A Simple Framework for Contrastive Learning of Visual Representations”, Blog post.